التاريخ
كيفية التعامل مع الجداول الإحصائية وتحويلها إلى رسوم بيانية – الجزء الثالث – تاريخ وجغرافيا – بكالوريا آداب
كيفية التعامل مع الجداول الإحصائية وتحويلها إلى رسوم بيانية – الجزء الثالث – تاريخ وجغرافيا – بكالوريا آداب
أولا: الرسم البياني بالأعمدة:
المعالجة البيانية للإحصائيات من خلال الرسم بالأعمدة:
يمكن أن تكون الأعمدة واحدة لوجود مؤشّر واحد بالجدول الإحصائي أو أكثر من مؤشّر وذلك كما يأتي:
الجدول الذي يتضمن متغير واحد / مؤشر واحد:
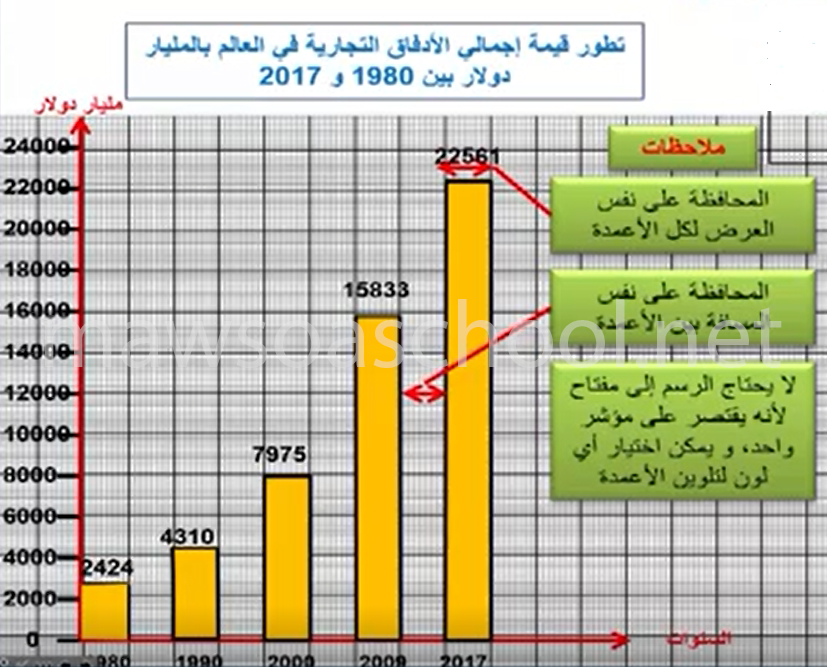
تطور قيمة إجمالي الأدفاق التجارية في العالم بالمليار دولار بين 1980 و 2017
| السنة | 1980 | 1990 | 2000 | 2009 | 2017 |
| إجمالي الأدفاق التجارية | 2424 | 4310 | 7975 | 15833 | 22561 |
طريقة العمل:
تحديد نوع الجدول : هو جدول متغير يحتوي على متغيرين فقط لذلك يخصص المحور العمودي للقيمة والمحور الأفقي للسنوات.
تحديد المقياس المناسب = القيمة الأكبر / طول المحور العمودي
التطبيق الحسابي: (20000 / 10 = 2000 إذن 1 صم = 2000 مليار دولار)
ملاحظة:
- نستخدم 20000 عوض 22561 لتفادي الفواصل.
- الجدول الذي يتضمن متغير واحد لا نضع له مفتاح.
- نضع عنوانا مناسبا للرسم البياني.
- المحافظة على نفس العرض لكل من الأعمدة.
- المحافظة على نفس المسافة بين الأعمدة
الجدول الذي يتضمن أكثر من متغير أو أكثر من مؤشر:
قيمة الاستثمار الأجنبي المباشر الوارد ورصيده ببعض دول الساحل الأفريقي سنة 2017 بالمليون دولار
| قيمة الاستثمار الوارد | رصيد الاستثمار الوارد | |
| بوركينا فاسو | 486 | 2863 |
| غمبيا | 87 | 412 |
| غينيا بيساو | 17 | 191 |
| مالي | 266 | 3989 |
| موريتانيا | 330 | 7079 |
| النيجر | 334 | 6372 |
| السنغال | 532 | 4858 |
| التشاد | 335 | 5439 |
طريقة العمل:
تحديد نوع الجدول : هو جدول متغير يحتوي على ثلاثة متغيرات فقط وهي:
(1) البلدان (2) قيمة الاستثمار الوارد (3) رصيد الاستثمار الوارد.
لذلك يخصص محورين عموديين أولهما لقيمة الاستثمار الوارد والثاني لرصيد الاستثمار الوارد وكل واحد منهما بلونينِ مختلفين. والمحور الأفقي للبلدان.

- نستخدم الطريقة نفسها في المثال السابق لتفادي الفواصل.
- الجدول الذي يتضمن أكثر من متغير نضع له مفتاح.
- نضع عنوانا مناسبا للرسم البياني.
- المحافظة على نفس العرض لكل من الأعمدة.
- المحافظة على نفس المسافة بين الأعمدة

ثانيا: تقنينة رسم المنحنى البياني:
هذه التقنية نعمل من خلالها على تمثيل ظاهرة معينة متطورة عبر السنوات، ورسم المنحنى البياني لا يتناسب إلا مع الجدول الإحصائي المتغير سواء يحتوي على متغير واحد أو أكثر من واحد، ولا يتناسب مع الجدول الثابت
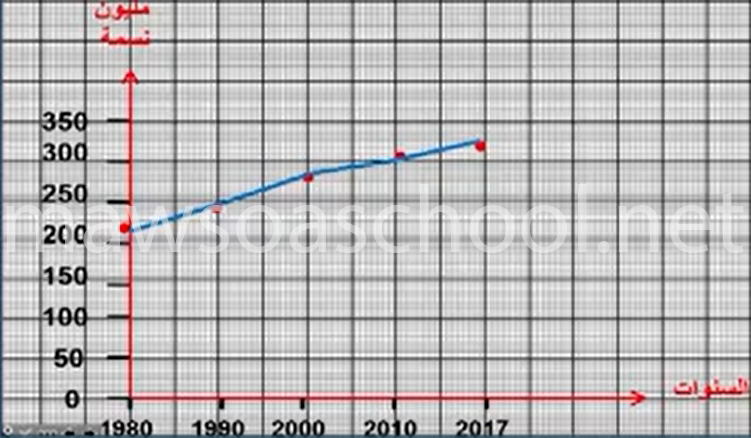
تطور عدد السكان بالولايات المتحدة الأمريكية بين سنتي 1980 و 2017 بحساب المليون نسمة
| السنوات | 1980 | 1990 | 2000 | 2010 | 2017 |
| عدد السكان | 227.2 | 249.6 | 282.1 | 309.3 | 325.7 |
طريقة العمل:
تحديد نوع الجدول : هو جدول إحصائي متغير يحتوي على متغير واحد فقط وهو:
عدد السكان؛ لذلك يخصص المحور العمودي لعدد السكان والمحور الأفقي للسنوات.
ومن ثم الشروع في تحديد عدد السكان في كل سنة وذلك بتحديد نقاط التقاطع على الرسم المنحنى البياني، وهي نقاط تقاطع بين المحور العمودي لعدد السكان والمحور الأفقي للسنوات والربط بين تلك النقاط.
ثالثا: الرسم بالأعمدة والرسم المنحنى معا:
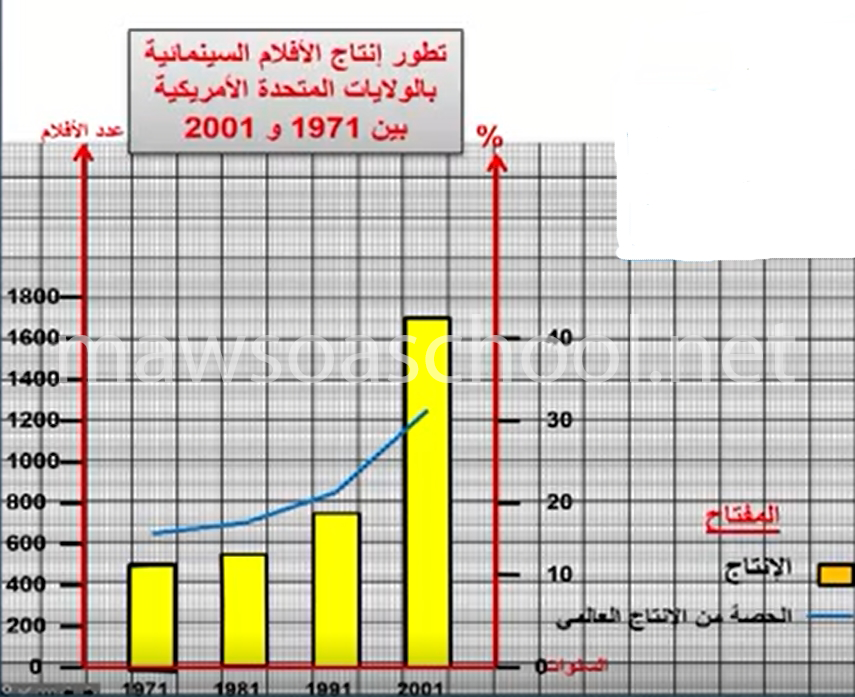
تطور إنتاج الأفلام السينمائية بالولايات المتحدة الأمريكية بين 1971 و 2001
| المؤشر | 1971 | 1981 | 1991 | 2001 |
| الإنتاج (عدد الأفلام) | 494 | 506 | 762 | 1740 |
| الحصة من الإنتاج العالمي | 16 % | 16.5 % | 21.5 % | 30.5 % |
المصدر: الكتاب المدرسي 04 ثانوي
طريقة العمل:
تحديد نوع الجدول : هو جدول إحصائي متغير يحتوي على متغيرين أي مؤشرين فقط وهما: الأول الإنتاج بالأرقام المطلقة والثاني الحصة من الإنتاج العالمي بالأرقام المائوية.
لذلك يخصص المحورين العموديين الأول الإنتاج بالأرقام المطلقة والثاني الحصة من الإنتاج العالمي بالأرقام المائوية، والمحور الأفقي للسنوات.
ومن ثم الشروع في تحديد عدد السكان في كل سنة وذلك بتحديد نقاط التقاطع على الرسم المنحنى البياني، وهي نقاط تقاطع بين المحور العمودي لعدد السكان والمحور الأفقي للسنوات والربط بين تلك النقاط
- الجدول الذي يتضمن أكثر من متغير نضع له مفتاح.
- نضع عنوانا مناسبا للرسم البياني.
- المحافظة على نفس العرض لكل من الأعمدة.
- المحافظة على نفس المسافة بين الأعمدة
رابعا: الرسم البياني الدائري:
يستعمل هذا النوع في بيان مدى توزع ظاهرة ما بين مختلف مكوناتها ومقارنتها، علاوة على أنه يجب أن يكون المجموع بالمائة يساوي 100 %
المثال التطبيقي: الرسم البياني الدائري:
بنية الناتج الداخلي الخام بالبرازيل سنة 2017
| القطاع | المساهمة في الناتج الداخلي الخام (%) | الدرجات |
| الفلاحة | 06 % | 21.6 |
| الصناعة | 27 % | 97.2 |
| الخدمات | 67 % | 241.2 |
| المجموع | 100 % | 360 |
أول خطوة نقوم بها هي تحويل النسبة المائوية إلى درجات وذلك عبر القاعدة التالية:
النسبة المائوية * 3.6
06 % * 3.6 = 21.6
27 % * 3.6 = 97.2
67 % * 3.6 = 241.2
100 % = 360 درجة
عملية الإنجاز كما يلي:
- نقوم أولا بتحديد مركز الدائرة.
- نقوم برسم الدائرة بواسطة البركار
- رسم الشعاع الذي سننطلق منه

نستعمل المنقلة حيث يجب أن يتوافق مركزها مع مركز الدائرة وخط درجة الصفرة على المنقلة يتوافق مع خطّ الشعاع.
نحدّد الدرجات التي قمنا بـتحديدها سابقا بوضع نقطة أمام كلّ درجة.

ربط النقطة التي حدّدنا بالنقطة المركزية وصولا إلى خطّ الدّائرة وهكذا نحدد الزاوية الاولى ونكتب عليها الدرجة التي تناسبها مع تلوينها ورسم مفتاحها في الآن.
نعيد نفس العملية في تحديد الزاوية الثانية ولا بدّ في هذا الانتقال لتحديد الزاوية الموالية الإنطلاق من أخر شعاع تمّ رسمه مع وضع المفتاح الثاني للزاوية الجديدة.
والزاوية الأخيرة لا حاجة في تحديدها لأن ما تبقّى من الدائرة يمثلها.
المثال التطبيقي: الرسم البياني النصف دائري:
أول خطوة نقوم بها هي تحويل النسبة المائوية إلى درجات وذلك عبر القاعدة التالية:
النسبة المائوية * 1.8
ثم نشرع في رسم وتحديد الوزايا باعتماد نفس التمشي السابق
للاطلاع على الجزء الثاني: اضغط هنا
للاطلاع على الجزء الاول: اضغط هنا
احصل على الدروس عن طريق البريد الالكتروني